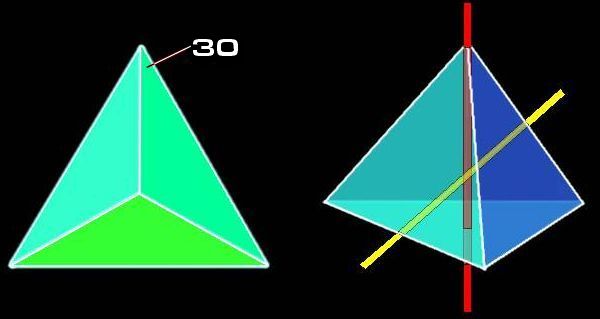The Tetrahedral World of Washington D.C.

c

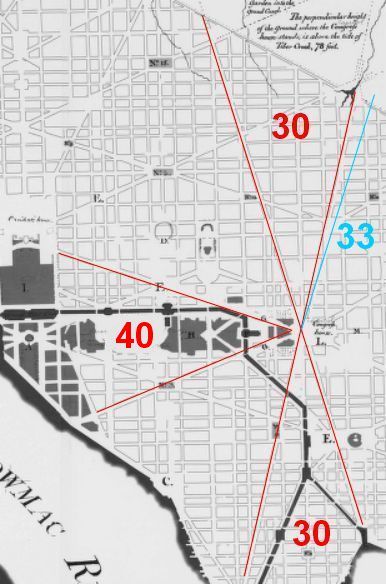
c

Part Two

This page continues Cydonia Quest's study into what Freemasonry Today describes as "the world's foremost Masonic City", (µµµ). The study of maps in the previous section revealed that within the grounds of the Capitol Pennsylvania and Maryland Avenues diverge from its western edge with an angle of 39 degrees before settling down to their more typical 40 degree divergence . As the coloured in satellite picture below shows the landscaping around the confluence of these two avenues has increasingly made them look like compass dividers - the most recognisable Masonic symbol. Perhaps Masons over the years have believed that the angle that the "dividers" are measuring is of significance.

C

ccccccccccccccccccccccccccccccccccc

c

We now turn our attention to L'Enfant's 1791 draft plan for Washington DC which is very little different from the way the city turned out. As the diagram below shows L'Enfant always seemed to have intended that the main lines of the west beam (Maryland and Pennsylvania Avenues) should diverge at 40 degrees - just as it has turned out today. The biggest surprise is that the north and south beams radiating from the Capitol were designed around lines intersecting at 30 degrees and not the 33 degrees that became the norm for the next few decades. There is one exception to this in that the north beam initially radiates from the Capitol at an angle of 33 degrees for a few blocks, before Delaware Avenue suddenly kinks due north for a short distance to rejoin and then follow the 30 degree line for the rest of its length. This 33 degree diversion is shown in blue in the diagram.

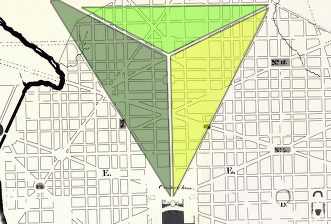
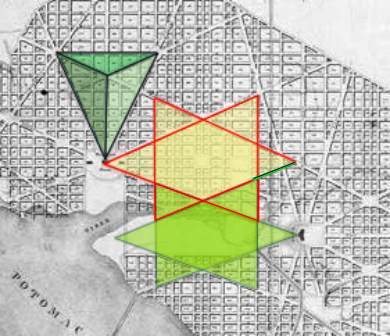
cccccccccccccccccccccccc

C

The initial 33 degree angle of divergence in the northern beam certainly fits in with the Enterprise Mission's thoughts on the use of tetrahedral geometry in Freemasonry. So is there anything in the main 30 and 40 degree angles for the Capitol beams in the 1791 draft that is consistent with tetrahedral geometry? There are in fact a number of things that can be suggested, of which the rotational geometry of tetrahedrons seems to be the most important.

(A) We may note that 4/3 = 1.33333 recurring. This gives us the harmonic decimal fraction of 33 that the Enterprise Mission finds so significant, (refer back to Part 1).

(B) As the diagram below-left shows the angle of 30 degrees is one that turns up quite frequently in tetrahedral and associated geometry. Viewed along any of its apexes, foreshortening causes the apparent angles within the visible facets of a tetrahedron to become three of 120 degrees and six of 30 degrees.

(C) To state the obvious, 40 degrees is nearly 39 degrees which is the doubling of the unique tetrahedral angle of 19.5 degrees. However, 40 degrees has a tetrahedral/Masonic significance all of its own. The geometrical emblem of the 33rd (and final) degree of Scottish Rite Freemasonry is a variant of the nonagram - (a nine pointed star created by joining up the points in a nine pointed shape or nonagon) - that involves the frames of three overlapping equilateral triangles. Although Freemasonry seems to have little to say in public about the geometrical significance of this figure, other esoteric groups are less reticent. It is just a case of joining the three triangular frames together to make the 3-D frame of a tetrahedron. (The fourth facet of the tetrahedron forms automatically when the other three triangular frames are assembled). So what has this to do with 40 degrees. Well the divergence angle between the stellations (points) in a regular nonagram is 40 degrees, (360/9 = 40). More will be said about the Masonic nonagram in Part Three. (See µµµ).

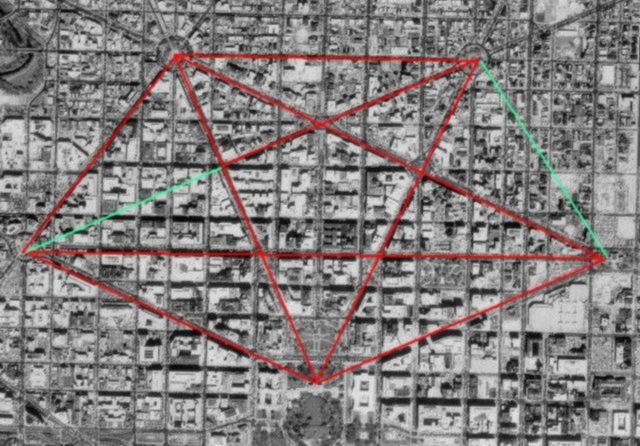
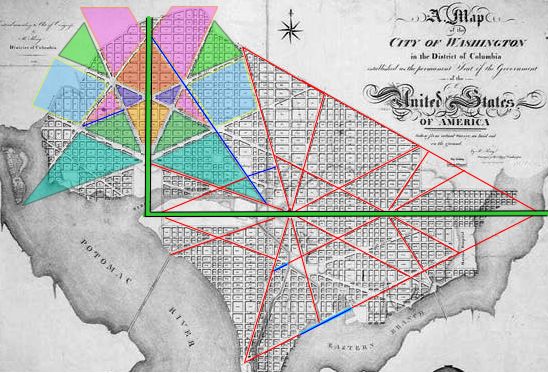
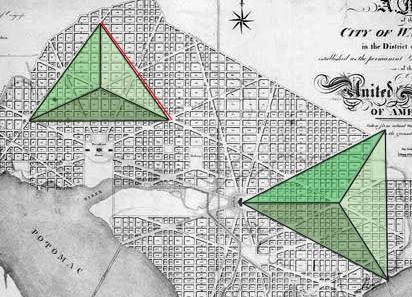
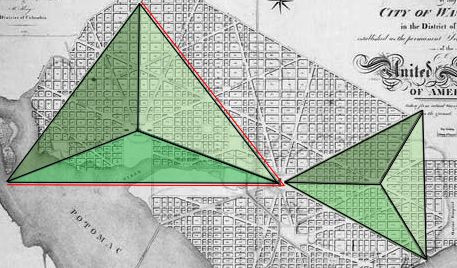
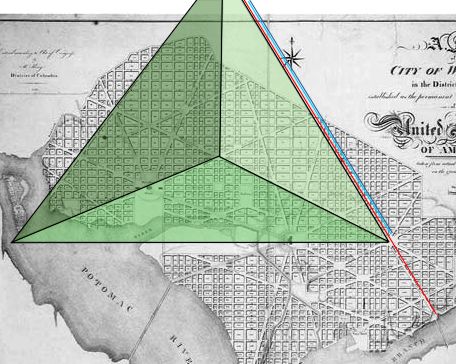
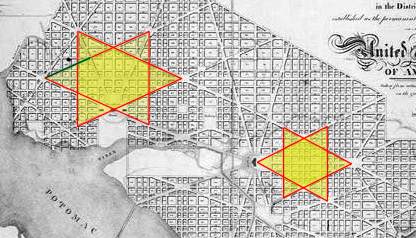
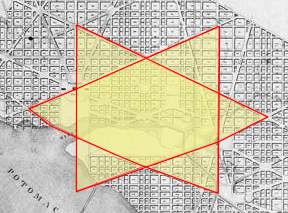
cccccccc

C

(D) A tetrahedron has 7 symmetrical axis of rotation. These seven axis are broken down into two families. As the red axis in the diagram above-right shows the most obvious way to create a symmetrical axis of rotation is to simply drive a line through an apex and out of the centre of the opposing facet. As there are 4 facets and 4 apexes in a tetrahedron there are 4 ways of doing this. The second method is less obvious. This involves driving a line through the middle of an edge and out through the middle of the opposing edge at a right angle to the first edge. This type of symmetrical axis of rotation is shown in yellow in the diagram. A tetrahedron has six edges, so there are only 3 axis of this type. (The following "stargates" lead to geometry web pages that allow the viewer to inter-actively rotate a tetrahedron about the two types of axis, see µµµ & µµµ).

We can note that in L'Enfant's draft plan of 1791 that the 30 degree beams and the 40 degree beams are proportionately consistent with the geometry of tetrahedral rotation. Noting that it would have been impractical for L'Enfant to have avenues diverging at angles of just 3 or 4 degrees if he intended that buildings should fit between them, 30 and 40 degrees would have been the next best thing. To spell it out, 3(0) + 4(0) = 7(0) or the 7 axis of rotational symmetry in a tetrahedron. Moreover the numbers involved with the Capitol beams, namely 3(0) and 4(0) are consistent with the two types of axial symmetry which are split 3 to 4.

There is of course no way of knowing whether L'Enfant intended that the north, south and west Capitol beams in his 1791 draft plan should follow tetrahedral numbers and angles. This work can only reveal the consistencies with tetrahedral geometry. L'Enfant's 1791 draft plan can be seen by clicking this "stargate" µµµ.

Before outlining further tetrahedral imagery in the L'Enfant plans for Washington DC it would be well to discuss....

.....Pierre Charles L'Enfant's Cunning Plan. At first glance L'Enfant's street plan for Washington DC looks a bit messy and it is tempting to think that the geometrical imagery observed in it arose by chance. Although some of the diagonal avenues in the plan are following some kind of symmetry, many others appear very random. This is not the case. By leaving out logical continuations of avenues and omitting the odd avenue altogether L'Enfant obscures his grand plan. This principle is shown in the following two diagrams.

If we take a look at the famous White House pentagram we find that only a single short road connection would have completed the surrounding pentagon and a logical extension of an avenue would have completed the pentagram itself. (The missing street segments are shown by green lines). It can also be seen that the completed geometrical figure is very symmetrical and has the White House at its point. This figure obviously did not arise accidentally but was put there by deliberate design.

C

cccccc

ccccccccccccccSatellite image courtesy of Keith Laney.

C

This pattern of symmetry is actually true for the whole of the street plan. In fact as the diagram below shows L'Enfant designed the whole of Washington around dual axis of symmetry. The first axis runs east/west through the Capitol and is marked by East Capitol Street. The second runs north/south through the White House and is marked by 16th Street.

In the diagram the two axis of symmetry are marked by thick green lines. I suspect that this right angled arrangement is supposed to symbolise the Masonic set-square. The symmetrical pattern of diagonal avenues around the east/west axis has been marked out in red. The eastward line of the northern boundary road has been extended outside the city boundary as have some avenues across the empty space of the Mall. Blue lines indicate illogical endings in some avenues or where one seems to plunge into the Potomac. It can be seen that most avenues are following an underlying plan of mirror symmetry - perhaps following the Hermetic dictum of "As above, so below".

In order to avoid confusion with the east/west arrangement, the symmetry around the north/south axis is high-lighted by the technique of colouring in the spaces between the avenues. The long, blue diagonal line indicates a route that would have completed the symmetry but where there is no avenue in the plan - another example of L'Enfant obscuring his underlying design. We will refer to this line as the "missing avenue" from now on. The reader will observe that the "missing avenue" completes the missing side of the White House pentagon.

C

ccccccccccccc

C

The street plan of Washington DC was not the result of giving a monkey pencils and a sheet of paper. It was the work of a French Masonic architect. There should be no reason to confuse the two, (see µµµ).

C

Tetrahedral Washington in All its Glory

We can now return to the further consideration of tetrahedral imagery in the L'Enfant plan. As the illustration below reveals, a combination of the "missing avenue" (indicated by the red shadowing) and the existing streets and avenues creates a tetrahedron image to the north of the White House. Whereas the Capitol tetrahedron points away from the rising Sun, this tetrahedron points away from the noonday Sun. Such sun alignments are important to the Freemasons because they were important to the ancient Egyptians.

C

ccccccccccccccccccccc

C

A combination of the "missing avenue", the east/west axis of symmetry (both shadowed in red) and L'Enfant's street plan creates a less satisfactory tetrahedral pyramid image, with the pinnacle hovering directly over the White House.

C

cccccccccccccccccc

C

It is also worth noting that L'Enfant's 1791 draft plan contained a few short diagonal avenues to the north of the White House (near the city boundary) which make a large "almost" tetrahedron that points at the President's House in much the same way as the White House Pentagram. The fact that the western facet doesn't quite match up may explain why these avenues were dropped from the plan.

C

Cccccccccccccccccccccccccc

C

There also appears to be a super tetrahedron hiding in the street plan. Most of this pyramid can be constructed by extending existing streets and avenues into the Potomac or outside the city boundary. However, the eastern edge of this tetrahedron is made by extending the line of Kentucky Avenue northwards. The blue line shows this "virtual" side to the tetrahedron which is so large its northern tip goes off the map.

c

ccccccccccccccccccc

c

The Washington Hexagrams. In the Anomalies Board discussion thread (that was one of the inspirations for this study) Keith Laney pointed out the existence in L'Enfant's street plan of a hexagram to the east of the Capitol building. This shares the same space as the "radiant tetrahedron of Capitol Hill". In fact there are many more hexagrams in the plan than this. The diagram below shows that not only is there a Capitol hexagram but that there is also a hexagram nestled over the White House in the same space as the White House pentagram. (The green line shows the location of the missing segment of avenue that is common to both these polygrams).

C

ccccccccccccccccccccc

c

The plan also connects the Capitol and the White House with the device of two interlocking hexagrams. In the illustration below the green hexagram is constructed merely by joining up the mirrored street pattern on the north and south sides of the open space of the Mall. This touches the Capitol on its western side. The yellow hexagram touches the White House on its eastern side. It is entirely made out of visible streets, with the exception of a short stretch of (illogically) missing avenue, which is shown by a green line. (We may also note that because the White House pentagram is enclosed in a pentagon that an elongated tetrahedron made out of the street plan touches its northern edge).

C

cccccccccccccccccccccccc

C

As the illustration below reveals the White House and Capitol Building are nestled opposite one another in a very large (if slightly crooked) hexagram that can be constructed just by joining up existing streets across the waters of the Potomac.

C

cccccccccccccccccccccccccccccc

c

In many of the geometry web pages I've visited the hexagram has been referred to as the "star tetrahedron". This is because the geometrists concerned have made the assumption that the hexagram is actually derived from a 2,500 year old interest in the Platonic Solids of Pythagoras. (Plato discovered the final solid). The Platonic Solids are the only regular faceted solids (hedrons) that can be enclosed in a sphere so that all the vertices touch the surface without penetrating it. One of the features of these polyhedra is that each one can be merged with another Platonic Solid to create a 3-D shape that can also be circumscribed perfectly within a sphere. This is known as "dualing". The tetrahedron is unique in that it is its own dual - so "as above, so below" - and the dual is known as the star tetrahedron.

c

ccccccccccccccccccccccccccccccccccccc

C

As the illustration above reveals the "star tetrahedron" is the three dimensional version of the hexagram. Trawls around the internet reveal that not only geometrists think of the hexagram as a two dimensional representation of the star tetrahedron. Many New Age websites also make the same assumption and imbue the "star tetrahedron" with wondrous magical properties. As will be seen in Part Three the hexagram is given three dimensional properties by the Freemasons using a circuitous route. It is a reasonable assumption that the hexagrams seen in L'Enfant's plans for Washington DC are yet another example of deliberate tetrahedral imagery.

µ Click "Stargate" to Return to Part One

µ Click "Stargate" to Proceed to Part Three

c

µ Return to The Conspiracy Latest Developments

µ Click "stargate" to return to The Conspiracy Part Three

µ Return to the Cydonia Quest main page